
Like geometry, topology is a branch of mathematics which studies shapes. From geometry to topology to differential topology Of course we do not stop here: the next hypersphere (the 4-sphere), is such that every region looks like 4-dimensional space, and so on in every dimension. But just like its lower dimensional cousins, the whole thing curves around on itself, in a way that flat 3-dimensional space does not, producing a shape with no sides, and only finite volume. We might be living in one now, for all we can see. So far, so predictable, but exactly the same thing is true for the first hypersphere (or 3-sphere): each region looks just like familiar 3-dimensional space. Again, these patches are sewn together in a way that leaves no edges, and has only finite area.
#Desmos 4d sphere Patch#
In the same way, each patch of the usual sphere (that is to say, the 2-sphere) looks like a patch of the 2-dimensional plane. The difference between the circle and the line is that when viewed from afar, the whole thing curves back to connect to itself, and has only finite length. What does this look like? Well, when we look at the circle from close up, each section looks like an ordinary 1-dimensional line (so the circle is also known as the 1-sphere). Now comes the exciting part, because exactly the same trick works in four dimensions, and produces the first hypersphere. If you do the same thing, but in 3-dimensional space, we get an ordinary sphere or globe.

If you choose a spot on the ground, and then mark all the points which are exactly 1cm away from it, the shape that emerges is a circle, with radius 1cm. But again, mathematical techniques can help, firstly by allowing us to generalise the phenomena that we do see in more familiar spaces.Īn important example is the sphere. Well that is fine, but how can such spaces be imagined? What does the lair of Yog-Sothoth actually look like? This is a much harder question to answer, since our brains are not wired to see in more dimensions than three. But mathematically, at least, as long as you believe in numbers, you don't have much choice but to believe in 4-dimensional space too. Of course this does not answer the physicist's question, of whether such dimensions have any objective physical existence. This procedure extends to all higher dimensions. Of course we can continue this line of thought: 4-dimensional space, for a mathematician, is identified with the sets of quadruples of real numbers, such as (5,6,3,2).
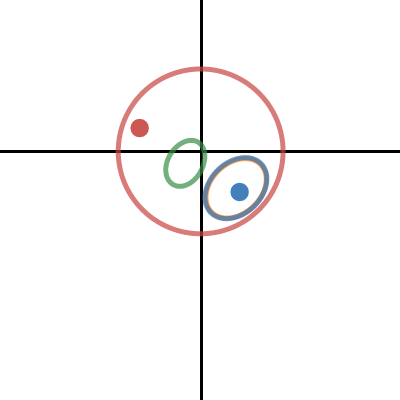
Just as a 2-dimensional plane can be described by pairs of coordinates such as (5,6) with reference to a pair of axes, so 3-dimensional space can be described by triples of numbers such as (5,6,3). Higher dimensions and hyperspheresĭo higher dimensions exist? Mathematics provides a surprisingly emphatic answer to this question. Over the last 50 years a subject called differential topology has grown up, and revealed just how alien these places are. Strange spheres really are the keys to higher dimensional worlds, and our understanding of them has increased greatly in recent years. But he could not have known how fortunate was the decision to represent Yog-Sothoth in this manner. Lovecraft had some interest in mathematics, and indeed used ideas such as hyperbolic geometry to lend extra strangeness to his stories (as Thomas Hull has discussed in Math Horizons). stupendous in its malign suggestiveness". Interestingly, on the rare occasions that Yog-Sothoth appears in the human realm, it takes the form of "a congeries of iridescent globes. In Lovecraft's mythology, the most terrible of these beings goes by the name of Yog-Sothoth. Lovecraft, these higher dimensions do indeed exist, and are home to all manner of evil creatures. Image by Claudio Rocchini, via Wikimedia Commons.Īccording to the early 20th century horror writer H.P. The curves are the projections of the hypersphere's parallels (red), meridians (blue) and so-called hypermeridians (green). This image comes from the projection of a 4-dimensional hypersphere. Just as a 3-dimensional object can be projected onto a 2-dimensional plane, so a 4-dimensional object can be projected onto 3-dimensional space.


 0 kommentar(er)
0 kommentar(er)
